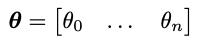High School Student Blog: Understanding Gradient Descent in AI (Part 1)

Gradient Descent — Demystified!!! (Part 1)

Gradient Descent is one of the most commonly used optimization algorithms implemented in Machine Learning problems. In this two-part mini-series, I will go over the following:

1. How does Batch Gradient Descent work?

2. What are the variations of Batch Gradient Descent?

3. How can we implement the Gradient Descent algorithms in Python?

Model Representation

Recall that for regression problems, we are taking input variables and mapping them out onto a continuous output by using some sort of hypothesis function.

This graph is an example of univariate linear regression (linear regression with one variable). We are predicting a single output value y from a single input value x.

Hypothesis Function

Univariate linear regression has the hypothesis function of the following form:

Y-hat is output of the hypothesis function with the form of theta_0 + theta_1*x1

This is equivalent to the equation of a line in the form of y = mx + b. Our hypothesis function is representing m and b as theta_0 and theta_1, respectively. Theta_0 and theta_1 are known as our parameters, as we feed these values into our hypothesis function in order to receive an output.

Example

Let’s assume that this is our set of training data.

Image Credit: Andrew Ng

Say we assign some random values for our parameters theta — let theta_0 be 2 and theta_1 be 2 . Our hypothesis function therefore becomes:

Hypothesis function after assigning parameters

This means that if we input 1 into our hypothesis function, our output y will be 4. This prediction is off by 3 because if you look at the table, the actual output for an input of 1 is 7.

With univariate linear regression, we are trying to find the optimal values of theta_0 and theta_1 that minimize this difference between predicted values and actual values in order to create a line of best fit.

Cost Function

Cost Functions can tell us the accuracy of our model. A higher cost means that our model made many errors and performed poorly, while a lower cost means that our model made infrequent errors and performed very well. There are many different types of cost functions, but for univariate linear regression, we shall use Mean Squared Error (MSE). Let’s call this cost function J.

Image Credit: freeCodeCamp

MSE for Univariate Linear Regression, with m training examples

Note: In ML notation, the superscripts with parentheses indicate which training example is being referenced (they don’t indicate exponents). For example x^(3) refers to the value of x for the third training example — it does not mean x cubed.

As shown above, we are summing up the squared differences between the actual values and predicted values for each training example m, and dividing this by the number of training examples (m) in order to get the mean.

But what about multivariate linear regression? Virtually every Machine Learning will have a multitude of parameters and inputs / features. To account for this, we can store these values into matrices.

Row vector of n parameters theta

Matrix for j training examples and n features

We can then rewrite our MSE equation using these matrices. Note that now our input for our cost function is now a vector of thetas.

MSE for Multivariate Linear Regression

Batch Gradient Descent

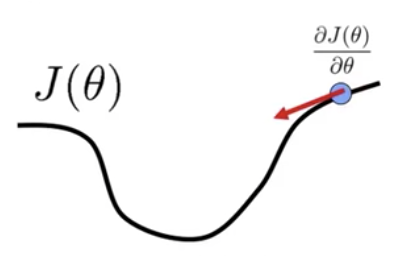
In order for our model to have the most accurate predictions as possible, we need to minimize the output of our cost function as much as possible. This is where Batch Gradient Descent comes into play. Batch Gradient Descent is an iterative optimization algorithm that allows us to find a minimum in our cost function.

Intuition

Imagine that you are a hiker — but you’re completely blind. You are trying to descend to the bottom of a mountain. How would you go about this? You would need to analyze the incline of the surface that you are walking on. As long as you are going downwards, you know you are going in the right direction. And as the incline gets flatter and flatter, you know that you are getting closer and closer to your destination.

Image Credit: Towards Data Science

This is the approach that batch gradient descent takes. The mountain is akin to the parameters and cost function plotted in space, the size of the steps you take is akin to the learning rate, and the incline of the mountain is akin to the gradient of the parameters, all of which is done iteratively. Furthermore, the bottom of the mountain is equivalent to a minimum value of the cost function.

But…What is a Gradient?

The gradient of function stores all the partial derivatives of a multivariable function into a vector. This vector tells us which direction increases the value of the function most rapidly. In Batch Gradient Descent, we use the gradient to determine how we should change our parameters so that our cost function decreases as much as possible. Thus, we look at the opposite direction of the gradient.

And What is the Learning Rate?

In order to determine our next point, we multiply the gradient by a number known as the learning rate or the step size. So if we have a gradient with a magnitude of 5.5 and a learning rate of .1, the algorithm will choose the next point that is .55 away from the previous point.

So, how do we choose the best learning rate? I will go into depth about that in the next article of this mini-series. But in general, if it’s too large, it can jump over the minima and back. And if it’s too small, many iterations will be required. Both of these result in the algorithm taking a long time to converge.

Image Source: Towards Data Science

The Math Behind Everything

If you find these next few sections to be a bit confusing, don’t worry. It’s not necessary to understand all the math in order to implement batch gradient descent: Scikit Learn and all the other coding libraries have taken care of it for us. However, I hope that you can get a general idea of what’s going on behind the scenes with this algorithm, rather than just providing you with a black box. First, take a look at the 2-D graph below.

Image Credit: Alexander Ihler

On the x-axis, we have our values of theta. On the y-axis, we have the output of our cost function after inputting theta. Our goal is to reach the minimum of this graph, where our cost is at its lowest. So how do we change theta so that we can decrease J(theta)? First, we must choose a direction in which J(theta) is decreasing. To do this, we look at the derivative of our cost function with respect to theta.

Image Credit: Alexander Ihler

Derivatives represent the slope of the tangent line of a specific point. If the derivative is positive, it means that the cost function is increasing. If it’s negative, it means that the cost function is decreasing (which is what we want).

But notice how this graph is two-dimensional, only displaying one value for a theta parameter. In reality our models are going to have many more values of theta. Thus, we need to generalize this to higher dimensions. To do this, we can take the gradient of our cost function, which measures the vector direction of steepest ascent.

Gradient Row Vector for Cost Function

Each entry for our vector represents the partial derivative of J with respect to each dimension. To decrease J, we take steps in the negative gradient direction until we find the local (or global) minima of the function.

The Algorithm

First, we initialize our parameters theta either by assigning them random values or by setting them all equal to 0.

Then, we find the gradient of J(theta) and update it based on the magnitude of the learning rate. The learning rate, symbolized by α, may remain constant or it may change throughout each iteration, depending on what the programmer wants to do.

To stop iterating this algorithm, we have some end conditions. If our cost is not changing sufficiently quickly or if our gradient is sufficiently small, the algorithm will come to a halt. Here is the pseudocode for Batch Gradient Descent:

Batch Gradient Descent Pseudocode

Batch Gradient Descent Algorithm for Linear Regression

To implement Batch Gradient Descent for linear regression, we need to first compute the gradient of our cost function J. Recall our MSE cost function for linear regression from before:

Let’s denote this error residual between the actual values and predicted values as e_m(theta).

We can now take the partial derivative of J with respect for each parameter. Below is the equation for when it’s with respect to our first parameter, theta_0.

Partial Derivative of our Cost Function with respect to theta_0 (our first parameter)

Now we need to evaluate the partial derivative of e_m(theta) at the end of the equation:

Thus, the partial derivative of our cost function with respect to theta_0 is:

We now do this for every other parameter theta. We shall store these in our gradient vector.

Using the distributive property, we can pull out these terms to write a more compact version of this vector:

We can also vectorize this expression to make it easier to implement in code:

All we need to do now is initialize our theta parameters and choose a learning rate before running the algorithm. After that, we are all good to go! Below is a great animation that illustrates the implementation of Batch Gradient Descent on Linear Regression:

Advantages of Batch Gradient Descent

1. Batch gradient descent can be vectorized, increasing the speed at which the training samples are processed.

2. Since every single training example is being analyzed before making a step in the negative gradient direction, the algorithm will generally make a stable convergence (assuming that the learning rate is not too high).

Disadvantages of Batch Gradient Descent

1. If there is a large number of training examples, batch gradient descent can be very computationally expensive and can therefore take a long time to converge.

2. The algorithm can easily converge in local minima when we are trying to reach the global minimum where the cost is at its lowest.

I hope that this article helps you understand the basics of Batch Gradient Descent! Next time, I’ll be teaching you about some of the variations of this algorithm — Stochastic Gradient Descent and Mini-Batch Gradient Descent.

If you are still a bit confused, I would recommend checking this video by StatQuest to get the basic idea. Some parts of this article have also inspired this video created by Professor Ihler of UCI, which I would also recommend you watch if you had any trouble with the math section of this article.

Advantages of Stochastic Gradient Descent

1. It is not very computationally expensive since there are only individual training examples that are being processed.

2. Unlike Batch Gradient Descent, SGD can get out of local minima due to its frequent updates and noisy steps.

Disadvantages of Stochastic Gradient Descent

1. Noisy steps can cause it to go in unfavorable directions.

2. It may take longer to converge due to these noisy steps.

3. Since the algorithm processes single training examples at a time rather than an aggregate of them, it cannot be put into a vectorized form.

An Introduction to Mini-Batch Gradient Descent

The Mini-Batch Gradient Descent Algorithm is another variation of the Batch Gradient Descent algorithm. Rather than calculating the gradient of the whole entire training set, Mini-Batch Gradient Descent splits the training dataset into smaller batches, and gradient descent is performed on each of these. It’s a sweet little compromise between Batch Gradient Descent and SGD!

References:

A couple of parts of the article were based on Machine Learning Mastery. I recommend checking him out — he has a blog that has a ton of content teaching ML/DL!

Kai Gangi is a Student Ambassador in the Inspirit AI Student Ambassadors Program. Inspirit AI is a pre-collegiate enrichment program that exposes curious high school students globally to AI through live online classes. Learn more at Inspirit AI

https://kaigangi72.medium.com/gradient-descent-demystified-part-2-7649ed2ba4d5